Did you solve it? Can you battle like a maths wizard?

Earlier today I set you the following four puzzles. Here they are again with solutions.

The questions were taken from a “maths battle”, which is a competitive event that mixes maths and debating. (For more info about maths battles, read the previous post.)

1. Four red dots

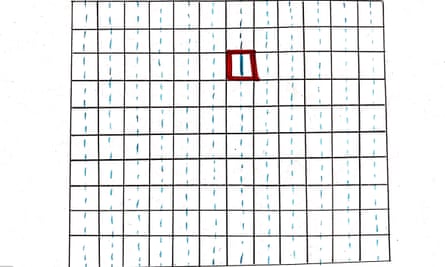
Find a way to draw red points on a sheet of A4 paper such that any circle of radius 1cm that you draw on that piece of paper will contain exactly four red points.

Solution Here’s one possible way. Draw parallel lines 1cm apart. When I wrote ‘points’ I may have misled you: the points are lines.

2. Square snip

A 10 x 12 rectangle is cut out of squared paper, as below, and folded along the lines several times to get a 1×1 square. If you were to cut this square in half, as also illustrated below, how many separate pieces of paper would you get?

Solution 11 or 13

Imagine that the square on the top of the folded paper is the red one below. The cut (blue) must extend up and down in a straight line, and likewise must be parallel through the middle all of the other squares. When you cut down these lines it leaves you with 13 pieces. If the original square was cut between the other two sides (i.e. the square was turned 90 degrees), you would get 11 pieces.

For the follow up question: draw out another 10x 12 grid and make a diagonal cut. Then follow this cut to the other squares. You will find that you get a grid of small squares with a diagonal of length 1, the centres of which are separated by length 2. Cut these out and (depending on which diagonal cut you made: NE, ES, SW, WN) you get 31, 36, 37 or 43 pieces.

3. Locky six

There are six locked suitcases and six keys for them. It is not known which keys are for which suitcase. What is the minimum number of attempts at unlocking suitcases that you need in order to guarantee you know which keys open which suitcases?

Solution 15 attempts

Take the first key and try to open five suitcases with it. If a suitcase opens this is great and we set that suitcase aside with that key. However, if the key doesn’t open any of the first five suitcases, this means it opens the sixth. We don’t need to waste another attempt on proving what we know is true, and we can set the sixth suitcase aside with its key. Now take another key and try to open each of these five suitcases in turn. Only four attempts are needed in order to determine which suitcase this key belongs to. Repeat this with the next key and so on. Therefore we need 5+4+3+2+1=15 attempts

4. Cube sabotage

Kathy has eight identical 1 x 1 x 1 yellow cubes. She wants to stack them together to make a 2 x 2 x 2 cube that is completely yellow on the outside. Peter wants to paint some of the faces of the 1 x 1 x 1 cubes purple. What is the smallest number of faces he needs to paint in order to prevent Kathy from being able to make her 2x2x2 cube completely yellow on the outside.

Follow-on: What if Kathy has 27 identical 1 x 1 x 1 cubes. How many faces does Paul need to paint to stop her making a 3 x 3 x 3 cube that is completely yellow on the outside.

Solution

Peter needs to paint only two (opposite) faces of a 1 x 1 x 1 cube. If the opposite faces are both purple, then one side of the 2 x 2 x 2 cube must be purple.

Paul needs paint two full cubes, which is 12 faces. If he painted only 11 faces, there is always a way for Kathy to hide the painted faces.

I hope you enjoyed today’s puzzles, I’ll be back on Boxing Day with some more.

Thanks to We Solve Problems for today’s questions. The organisation runs maths battles in the UK. Again, to read more about these fantastic competitions, see the previous post.

I set a puzzle here every two weeks on a Monday. I’m always on the look-out for great puzzles. If you would like to suggest one, email me.

I give school talks about maths and puzzles (online and in person). If your school is interested please get in touch.