Can you address it? Prisoners and containers

Today’s puzzle will involve two prisoners. Let’s contact them Piper and Alex. You will be asked to find a tactic that wins them their liberty.

Puzzles about jail escape strategies are a relatively new style of mathematical challenge, only a few decades old. They emerged from laptop science. A prison – a put in which accessibility to details is restricted – is a great location for puzzles about the successful interaction of information.

The answer to today’s puzzle will blow your brain. Lock me up if it doesn’t.

Now again to Piper and Alex.

The four bins

Piper and Alex share the same cell. A guard arrives in and tells them that they are to be established a challenge that could earn them their flexibility. It includes the two prisoners getting taken one particular right after the other into a different mobile exactly where there are four similar empty packing containers, numbered 1, 2, 3 and 4. The procedure is as follows:

i) Piper will be led into the new mobile. The guard will then take a piece of paper from his pocket and randomly put it into just one of the four packing containers. Piper will see which box the paper is in. The guard will shut the bins. He will flip a coin and spot it on Box 1. He will flip another coin and put it on Box 2, and so on for Boxes 3 and 4. Each coin has a 50/50 likelihood of staying heads or tails. Piper will be ready to see the faces of all cash.

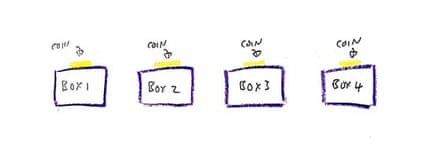
ii) Piper should switch a one coin over. (She can pick any just one of the four coins, and when she does, a head gets to be a tail, or vice versa.) She will then be led out the mobile and taken to a third cell on her personal.

iii) Alex is now taken into the cell with the boxes. She will not be capable to see within the bins because they are closed. But she will be capable to see the faces of the cash. She will be questioned to open a box. If the box has the paper in it both equally prisoners are freed. If it does not have the paper in it, the prisoners are returned to their cell.

What technique guarantees that the prisoners will acquire their liberty?

The prisoners are permitted to talk about their method just before Piper is taken into the mobile with the boxes, and settle on a prepare. But once Piper goes into that mobile she has no communication with Alex, apart from the ‘message’ that she presents by turning in excess of a one coin.

This is an astounding puzzle because it appears to be totally difficult that there is a way Piper can express to Alex with a solitary coin which box has the paper in it when she desires to choose into consideration the four possible destinations and 16 probable combos of heads and tails. You will marvel at the outcome when you see it.

Like lots of puzzles, the way to deal with this 1 is to simplify the condition, to see if any insights leap out. Let’s do that. Try to remedy just the same puzzle when there are only two bins in the mobile. That is, Piper will be led into a place with only TWO packing containers. The guard goes by way of the rigmarole of placing the paper in just one of the containers, and placing a coin randomly on each and every box. Each individual coin has a 50/50 prospect of becoming heads or tails. Piper will be equipped to see the faces of each cash.

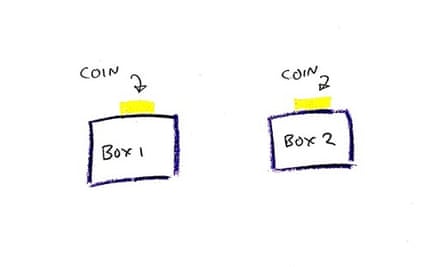
When there are only two boxes, how does Piper connect which box has the paper by turning about only a person coin?

In other words, what technique ensures that the prisoners will gain their liberty?

If you resolve the two-box edition, you’ll be executing properly. If you clear up the four-box version, you are leading of the course.

I’ll be back at 5pm Uk with the solutions. In the meantime, NO SPOILERS. In its place focus on your favorite jail movies and which two prisoners you consider would have experienced the best likelihood of resolving this puzzle.

Many thanks to Pierre Chardaire, a retired personal computer scientist, who wrote the puzzle.

I set a puzzle right here every two weeks on a Monday. I’m generally on the look-out for terrific puzzles. If you would like to propose just one, e-mail me.

I give college talks about maths and puzzles (on the web and in individual). If your university is interested make sure you get in touch.